seik.in

新みそきん発売まであと-2450667.988秒

"meta": { "date": "2025-05-18 12:00:00", }

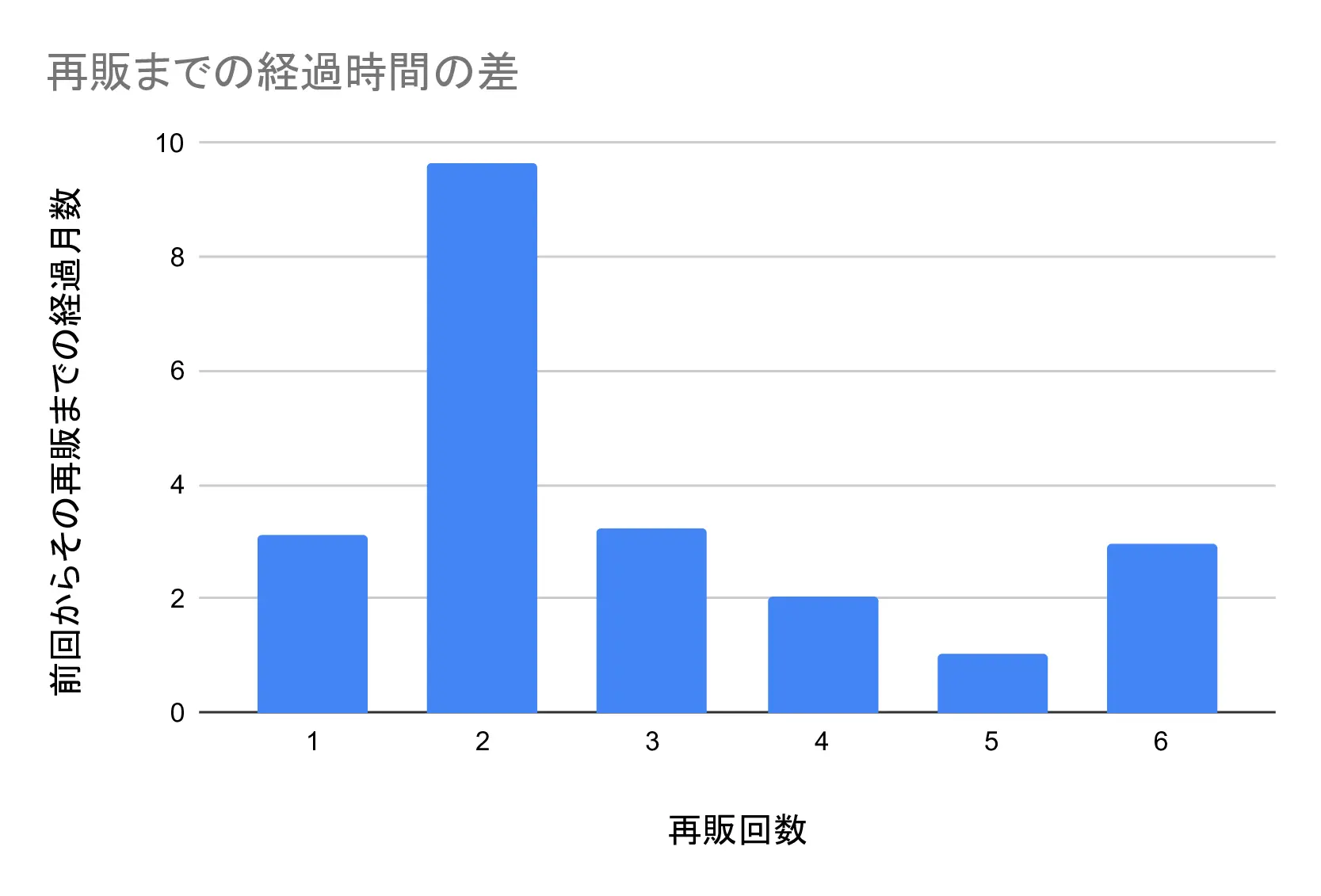
みそきんの再販間隔のグラフ

みそきんの再販間隔を調べる。 みそきんの各発売日はUnix時で以下の通りである。 なお、各発売日を t n t_n で記し、 n n は再販回数を示す。また、単位は [ s ] \mathrm{[s]} である。

t 0 = 1683558000 t 1 = 1691593200 t 2 = 1716598800 t 3 = 1724979600 t 4 = 1730250000 t 5 = 1732928400 t 6 = 1740618000 t_0 = 1683558000 \\ t_1 = 1691593200 \\ t_2 = 1716598800 \\ t_3 = 1724979600 \\ t_4 = 1730250000 \\ t_5 = 1732928400 \\ t_6 = 1740618000

これより、各発売日間隔 Δ t m \Delta t_m は m ≥ 1 m \geq 1 として

Δ t m = t m − t m − 1 \Delta t_m = t_m - t_{m-1}

として

Δ t 1 = 8035200 Δ t 2 = 25005600 Δ t 3 = 8380800 Δ t 4 = 5270400 Δ t 5 = 2678400 Δ t 6 = 7689600 \Delta t_1 = 8035200 \\ \Delta t_2 = 25005600 \\ \Delta t_3 = 8380800 \\ \Delta t_4 = 5270400 \\ \Delta t_5 = 2678400 \\ \Delta t_6 = 7689600 \\

となる。単位を月に直すには

Δ t n [ s ] = Δ t n 60 ⋅ 60 ⋅ 24 ⋅ 30 [ m o n t h ] \Delta t_n\mathrm{[s]}=\frac{\Delta t_n}{60\cdot 60 \cdot 24 \cdot 30}\mathrm{[month]}

を計算する。これを図示したものを以下に示す。

再販までの月数グラフ

影響の伝搬

注意！こっからクソ適当になります。

さて、ここから人が感じたであろう実質的な待ち時間 t w a i t ( t ) t_\mathrm{wait}(t) を求める。1つの販売あたりの実施日数を N n N_n とすると、各値は以下のようになる。

N 0 = 1 N 1 = 1 N 2 = 2 N 3 = 1 N 4 = 1 N 5 = 1 N 6 = 2 N_0 = 1 \\ N_1 = 1 \\ N_2 = 2 \\ N_3 = 1 \\ N_4 = 1 \\ N_5 = 1 \\ N_6 = 2 \\

ここから、再販回数 n n での単位時間あたりの販売回数をみそきん再販密度 ρ n \rho_n として計算する。

ρ n = { N n − 1 Δ t n [ n ≠ 0 ] N 1 Δ t 0 [ n = 0 ] \rho_n =\left\lbrace \begin{align*} \frac{N_{n-1}}{\Delta t_n} & [n \neq 0] \\ \frac{N_{1}}{\Delta t_0} & [n = 0] \end{align*} \right.

ここで、拡散を考える式 D ( t ) D(t) を導入し、ある時間 t t において各再販がみそきんを求める人にどれだけの影響を与えるかを考える。 密度の考えかたを導入すれば、単位体積・融和することを仮定したときの密度の和は全て足し合わせたものからその個数 ν \nu を割ることで考えられるので、

ρ a l l ( t ) = 1 ν ∑ i = 0 ν ρ i ⋅ D i ( t ) \rho_\mathrm{all}(t) = \frac{1}{\nu}\sum_{i=0}^{\nu} \rho_i\cdot D_i(t)

そして、この全みそきん再販密度 ρ a l l \rho_\mathrm{all} は逆数を取れば再販を待つ人の待機時間 t w a i t ( t ) t_\mathrm{wait}(t) となる。

t w a i t ( t ) = 1 ρ a l l ( t ) t_\mathrm{wait}(t) = \frac{1}{\rho_\mathrm{all}(t)}

今度は拡散の式 D ( t ) D(t) の内容を考える。拡散のええ感じの基本式は

exp ⁡ ( − t 2 ) \exp\left(-t^2\right)

で表される気がするので、その広がりが Δ t \Delta t 全ての平均 Δ t ‾ \overline{\Delta t} にするとして

Δ t ‾ = 1 ν ∑ i = 0 ν Δ t i \overline{\Delta t} = \frac{1}{\nu}\sum_{i=0}^\nu \Delta t_i

となり、拡散の式は

exp ⁡ ( − t 2 Δ t ‾ ) \exp\left(-\frac{t^2}{\overline{\Delta t}}\right)

になりそうで、そこから再販が生じる時間までの差分を考えると

D i ( t ) = exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) D_i(t) = \exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right)

となる。ここで、このサンプルでは D j ( t ) D_j(t) が j j にかかわらず全て0に近しい値をとりうるので ρ a l l ( t ) \rho_\mathrm{all}(t) が極めて大きくなる恐れがある。 よって調整する係数 b b を導入して、

D i ( t ) = ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) ( 0 ≤ b ≤ 1 ) D_i(t) = (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right)\\ (0 \leq b \leq 1)

として調整を行う。さらに、発表前と発表後の待ちの感情の拡散度合いが等しいことは考えられない(未来予知し、もう出るやろなぁ……安心しよとなっていることになる)ので、拡散を一旦片側のみにする。

D i ( t ) = u ( t i − t 0 ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) } ( 0 ≤ b ≤ 1 ) u ( τ ) = { 0 ( τ < 0 ) 1 ( τ ≥ 1 ) D_i(t) = u(t_i-t_0)\cdot\left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right) \right\rbrace \\ (0 \leq b \leq 1)\\ u(\tau) = \left\lbrace \begin{align*} 0 &&(\tau < 0) \\ 1 &&(\tau \geq 1) \end{align*} \right.

また、平均もそれまでの個数を考えるようにして、

Δ t ‾ = ∑ i = 0 ν u ( t i − t 0 ) ⋅ Δ t i ∑ i = 0 ν u ( t i − t 0 ) \overline{\Delta t} = \frac{\displaystyle \sum_{i=0}^\nu u(t_i-t_0) \cdot \Delta t_i}{\displaystyle \sum_{i=0}^\nu u(t_i-t_0)}

となる。こうして拡散と平均が不連続となった。 これは発表されてから発売されるまでの待ちが考慮されていないためである。よって、ここでは発表から発売日までの時間差 τ d e p . \tau_\mathrm{dep.} を導入して

D i ( t ) = u ( t 0 − t i ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 τ d e p . ) } + u ( t i − t 0 ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) } ( 0 ≤ b ≤ 1 , τ d e p . ≥ 0 ) Δ t ‾ = ∑ i = 0 ν u ( t i − t 0 ) ⋅ Δ t i ∑ i = 0 ν { u ( t 0 − t i ) ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 τ d e p . ) + u ( t i − t 0 ) } \begin{gather*} D_i(t) = u(t_0-t_i)\cdot \left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\tau_\mathrm{dep.}}\right) \right\rbrace\\ + u(t_i-t_0)\cdot\left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right) \right\rbrace \\ \end{gather*} \\ (0 \leq b \leq 1,\quad \tau_\mathrm{dep.} \geq 0)\\ \overline{\Delta t} = \frac{\displaystyle \sum_{i=0}^\nu u(t_i-t_0) \cdot \Delta t_i}{\displaystyle \sum_{i=0}^\nu \left\lbrace u(t_0-t_i) \cdot \exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\tau_\mathrm{dep.}}\right) + u(t_i-t_0) \right\rbrace}

と表現することとする。これで連続な結果が得られる。 最後に、初期値が微小から始まることを考慮する初期修正係数 a a を導入し、

D i ( t ) = a ⋅ { 1 − exp ⁡ ( t Δ t ‾ ) } × ( u ( t 0 − t i ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 τ d e p . ) } + u ( t i − t 0 ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) } ) ( a ≥ 1 , 0 ≤ b ≤ 1 , τ d e p . ≥ 0 ) \begin{gather*} D_i(t) = a \cdot \left\lbrace 1-\exp\left(\frac{t}{\overline{\Delta t}}\right) \right\rbrace \\ \times \Bigg( u(t_0-t_i)\cdot \left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\tau_\mathrm{dep.}}\right) \right\rbrace\\ \qquad + u(t_i-t_0)\cdot\left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right) \right\rbrace \Bigg) \\ \end{gather*} \\ (a\geq 1 ,\quad 0 \leq b \leq 1,\quad \tau_\mathrm{dep.} \geq 0)\\

となる。

全てまとめると、

t w a i t ( t ) = 1 ρ a l l ( t ) ρ n = { N n − 1 Δ t n [ n ≠ 0 ] N 1 Δ t 0 [ n = 0 ] ρ a l l ( t ) = 1 ν ∑ i = 0 ν ρ i ⋅ D i ( t ) D i ( t ) = a ⋅ { 1 − exp ⁡ ( t Δ t ‾ ) } × ( u ( t 0 − t i ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 τ d e p . ) } + u ( t i − t 0 ) ⋅ { ( 1 − b ) + b ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 Δ t ‾ ) } ) ( a ≥ 1 , 0 ≤ b ≤ 1 , τ d e p . ≥ 0 ) Δ t ‾ = ∑ i = 0 ν u ( t i − t 0 ) ⋅ Δ t i ∑ i = 0 ν { u ( t 0 − t i ) ⋅ exp ⁡ ( − { t − ( t i − t 0 ) } 2 τ d e p . ) + u ( t i − t 0 ) } \begin{gather} t_\mathrm{wait}(t) = \frac{1}{\rho_\mathrm{all}(t)}\\ \rho_n =\left\lbrace \begin{align*} \frac{N_{n-1}}{\Delta t_n} & [n \neq 0] \\ \frac{N_{1}}{\Delta t_0} & [n = 0] \end{align*} \right.\\ \rho_\mathrm{all}(t) = \frac{1}{\nu}\sum_{i=0}^{\nu} \rho_i\cdot D_i(t)\\ \begin{gather*} D_i(t) = a \cdot \left\lbrace 1-\exp\left(\frac{t}{\overline{\Delta t}}\right) \right\rbrace \\ \times \Bigg( u(t_0-t_i)\cdot \left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\tau_\mathrm{dep.}}\right) \right\rbrace\\ \qquad + u(t_i-t_0)\cdot\left\lbrace (1-b)+b\cdot\exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\overline{\Delta t}}\right) \right\rbrace \Bigg) \\ \end{gather*} \\ (a\geq 1 ,\quad 0 \leq b \leq 1,\quad \tau_\mathrm{dep.} \geq 0)\\ \overline{\Delta t} = \frac{\displaystyle \sum_{i=0}^\nu u(t_i-t_0) \cdot \Delta t_i}{\displaystyle \sum_{i=0}^\nu \left\lbrace u(t_0-t_i) \cdot \exp\left(-\frac{\big\lbrace t-(t_i-t_0)\big\rbrace ^2}{\tau_\mathrm{dep.}}\right) + u(t_i-t_0) \right\rbrace} \end{gather}

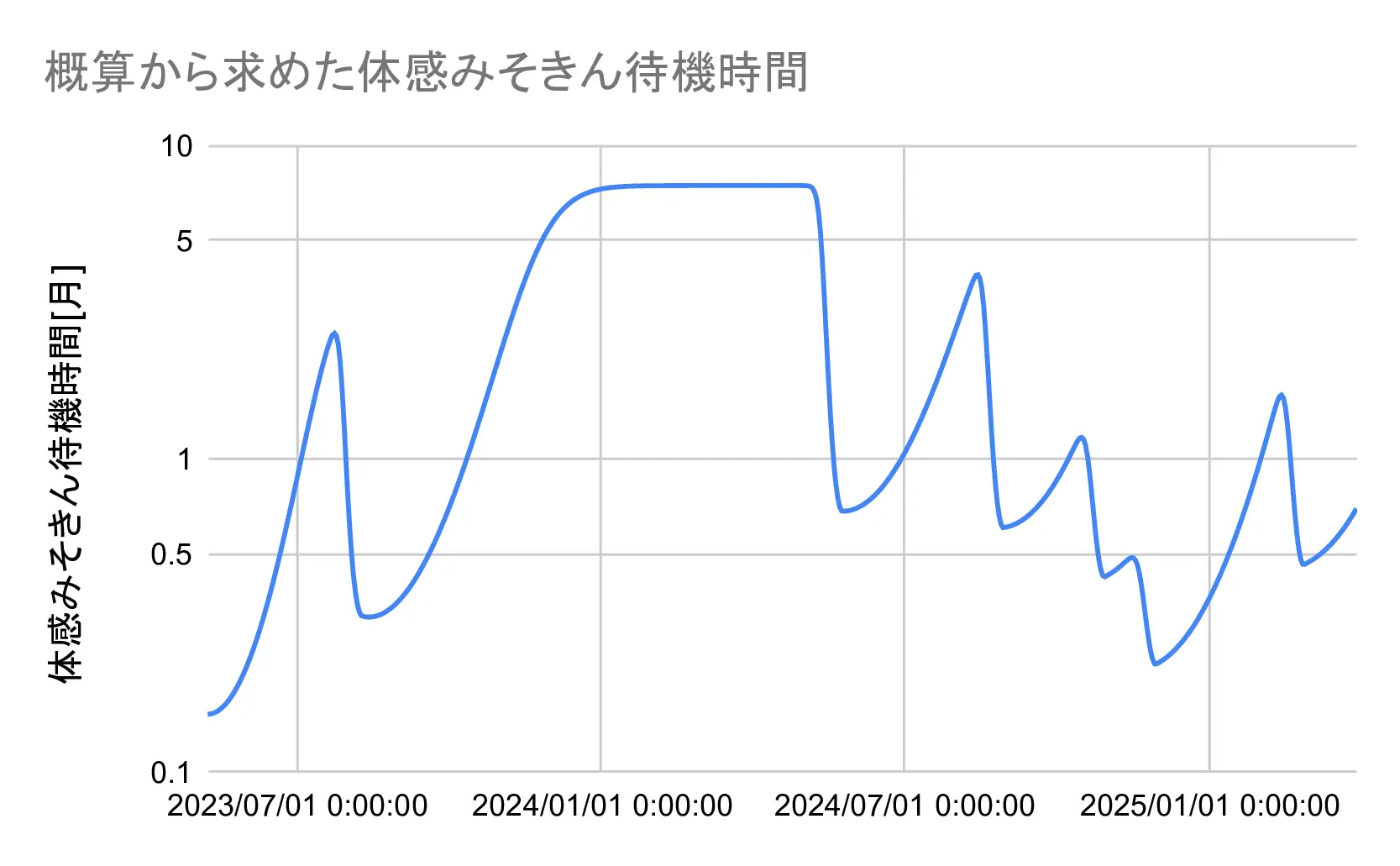
で、これを数値計算で求めれば、これまでの期間の人が感じたみそきん待機時間の概算ができる……かも？

a = 20 , b = 0.9955 , τ d e p . = 2 [ w e e k ] = 14 [ d a y ] = 1209600 [ s ] a = 20,\quad b = 0.9955, \quad \tau_\mathrm{dep.}=2[\mathrm{week}]=14[\mathrm{day}]=1209600[\mathrm{s}] とすると、数値計算で求まったグラフは以下のようになる

再販に対する人々の待機時間モデルの数値計算グラフ